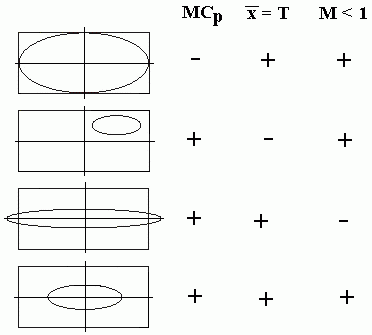
Doc. RNDr. Josef Tošenovský, CSc.
Katedra kontroly a řízení jakosti, VŠB-TU Ostrava
5. Sledujete více ukazatelů kvality současně?
Pak není správné hodnotit způsobilost u každého ukazatele samostatně.
Jak se hodnotí způsobilost u více ukazatelů způsobilosti?
Pomocí vícerozměrných indexů.
Kdy je přípustné hodnotit každý ukazatel
kvality samostatně?
Jsou-li navzájem nezávislé.
Příklad:
Je-li pro proměnné X1, X2 (tabulka 1) stanovena specifikace:
LSL1 =
136, T1 = 176, USL1 = 216 a LSL2 = 41, T2 = 53,
USL2 = 62.5, vychází
pro X1: Cpm = 0.724 a pro X2: 0.542, tedy v obou případech nezpůsobilost,
zatímco vícerozměrný index MCpm = 0.995, přičemž MCpm(min) = 0.86 což znamená,
že proces je způsobilý.
Tabulka 1: Hypotetická data
Pozn.: U indexu MCpm i hodnota menší než 1 může být dostatečná.
Jaké jsou zde obecné požadavky pro hodnocení způsobilosti?
Jsou to tyto požadavky:
a) Stabilita procesu: Ověří se pomocí vícerozměrného regulačního diagramu nebo speciálním testem stability.
b) Korektní data:
Měla by být:
- reprezentativní,
- nezávislá (ověří se testem),
- bez odlehlých hodnot (ověří se testem).
c) Správná tolerance.
d) Normalita (ověří se testem na vícerozměrnou normalitu).
Co se u vícerozměrných ukazatelů kvality hodnotí:
a) způsobilost, b) centrování
procesu, c) umístění výsledků
měření
(MCp, MCpm)
(t - test)
(statistika M)
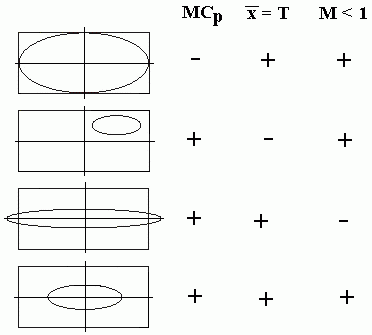
Je možné u vícerozměrného ukazatele kvality používat grafické metody ?
Na obr.
2 je dvourozměrný ukazatel kvality s normálním rozdělením,
na obr. 3 pohled do roviny X1 O X2 s vymezením tolerančního intervalu pro X1 a
X2, cílovou hodnotou T1 a T2, centrálním bodem o souřadnicích a cílovým
bodem.
Hodnotí se významnost odchylky těchto dvou bodů, variabilita v tolerančním
obdélníku, který je vymezen intervaly (LSL1,USL1), (LSL2,USL2) a odlehlost
(body mimo toleranční obdélník):
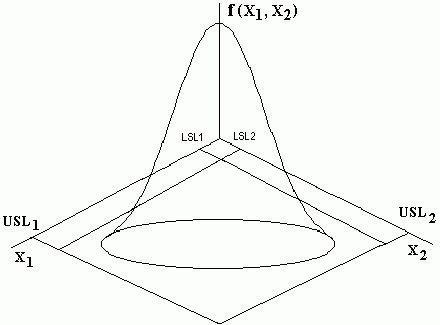
Obr. 2: Dvourozměrný ukazatel kvality s
normálním rozdělením.
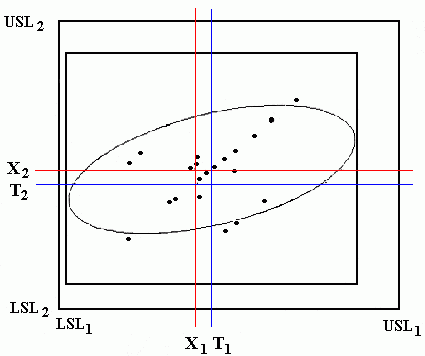
Obr. 3: Pohled do roviny x1Ox2 s vymezením tolerančního intervalu pro
x1 a x2, cílovou hodnotou T1 a T2.
6. Je možné u kusové výroby počítat index způsobilosti ?
U kusové výroby se při hodnocení způsobilosti počítá procentuální využití tolerance pomocí vztahu:
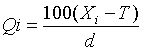
d = tolerance
Xi = dosažená hodnota ukazatele kvality
T = předepsaná (cílová) hodnota ukazatele kvality
Qi = procentuální využití tolerance (zde symetrické)
Příklad
Toleranční interval je vymezen hranicemi: LSL = 5, USL = 10 a
T = 7.5.
Bylo-li dosaženo hodnoty X = 7, je Q = - 20% využití tolerance (znaménko
mínus určuje pouze orientaci dosažené hodnoty vlevo od T).
Je-li X = 9.5, bude Q = 80% a pro X = USL = 10 je
Q = 100%.
Qi se počítá pro xmax a xmin.
Program počítá také průměrnou absolutní hodnotu Qi , která je užitečná,
je-li provedeno více než jedno měření. Ve výsledcích programu Capa je označena
E|Q|.
Pro dvě měření X = 7 a X = 9.5 je průměrné využití tolerance E|Q|
= 50 .
Počítá se také index způsobilosti CpT podle původního vzorce, připraveného
pro tento program.
Zde, pro X = 7, vychází CpT = 5.0.
Závěr
Problémy, o kterých jsme hovořili v našem seriálu o hodnocení způsobilosti, jsou jen některé z mnoha, které se vyskytují. Praxe však přináší mnoho dalších otázek, například:
- Kdy lze použít index Cpk?
- Jaké jsou podmínky pro jeho použití?
- Jak se prověří jejich splnění?
- A jak se postupuje, když splněné nejsou?
- Co se stane, budete-li ignorovat předepsané požadavky?
- Koho hlavně postihnou nedůslednosti v hodnocení způsobilosti: odběratele nebo dodavatele?
- Co všechno lze z vypočítaného indexu zjistit?
- Co je to komplexní hodnocení způsobilosti?
- Co by mělo předcházet a co následovat (před /po) výpočtu indexu způsobilosti?
- Používají se při hodnocení způsobilosti také grafické metody?
- Jakou roli hraje typ tolerance?
- A co vícerozměrné ukazatele kvality, jak tam se hodnotí způsobilost?
- Jak hodnotit způsobilost u kusové výroby?
- Jaké "triky" zkoušejí dodavatelé při vykazování způsobilosti a jak je odhalit?
- Je možné hodnotit způsobilost při kontrole kalibrací, tedy bez měření?
- Jak hodnotit komplexně způsobilost u výrobků, u kterých se sleduje více nezávislých znaků kvality?
Na tyto a další otázky můžete najít odpověď v učebnici Tošenovský,J.,
Noskievičová,D.: "Statistické metody pro zlepšování jakosti", Montanex
a.s. 2000. Praktické řešení uvedených problémů nabízí náš nový program
Capa.
Podrobnosti o možnostech získání programu získáte v nakladatelství
Montanex, nebo prostřednictvím emailové adresy: josef.tosenovsky@vsb.cz.
Program Capa je určen k hodnocení způsobilosti pro jakoukoli vyskytující
se situaci.
Členění programu (dostupný graf)
1 Jednorozměrné indexy 1.1 N-rozdělení 1.1.1 Symetrická tolerance (G1) 1.1.2 Nesymetrická tolerance (G1) 1.1.3 Jednostranně neomezená tolerance (G1) 1.1.4 Poloviční tolerance 1.1.5 Tolerance typu S 1.2 No-N rozdělení 1.2.1 Clementsova metoda 1.2.2 Castagliolova metoda (G5) 1.2.3 Intervalový odhad Cpk metodou bootstrap 1.2.4 Kusová výroba 1.2.5 Indexy Cpp, CpT 2 Testování indexu 2.1 Test Cpm 2.1.1 Průměr = T 2.1.2 Průměr různý od 2.1.3 Test C*pm 2.2 Test: průměr = T 3 Vícerozměrné index 3.1 Vektory Cpm, Cp 3.2 Vícerozměrná normalita 3.2.1 Centralizace procesu 3.2.2 Vybočující hodnoty (G3) 3.3 Vícerozměrný index MCpm, MCp 4 Ztrátová funkce 4.1 N-tolerance symetrická 4.2 N-tolerance nesymetrická 4.3 S-tolerance 4.4 L-tolerance 5 Testy 5.1 Test normality porovnáním šikmosti a špičatosti (G2) 5.2 Test normality Shapiro Wilk (G2) 5.3 Test normality Anderson-Darling (G2) 5.4 Test předpokladu o střední hodnotě 5.5 Test stability procesu (nahradí regulační diagram) 5.6 Test nezávislosti dat
V závorce je uvedeno, které grafické metody jsou k dispozici pro danou kapitolu. Jedná se o tyto komplexy grafických metod:
G1: Histogram, Gaussova křivka pro parametry daného souboru, průměr ,
pravidlo „3 sigma“, tolerance (LSL,USL), cílová hodnota T.
G2: Q-Q graf. pro grafické posouzení normality + toleranční interval.
G3: Dvourozměrný vektor způsobilosti vymezující oblast, kde by se měly
nacházet všechny hodnoty a oblast, kde skutečně jsou.
G4: Odlehlé hodnoty.
Pro jednorozměrný ukazatel kvality je graficky vymezena oblast, kde
by měly být všechny naměřené hodnoty (Grubbsův test).
Měření překračující stanovené meze jsou odlehlé hodnoty a mohou být
vyřazeny.
G5: Castagliolova metoda.
Znázorňuje body empirické distribuční funkce a jejich barevnou aproximaci
polynomy různých stupňů. Nalezená empirická distribuční funkce je použita
v numerické části programu k odhadu indexu CpK pro libovolný typ rozdělení.
Představu o tomto programu si můžete udělat na základě demoverze. Demoverzi tohoto programu vám na požádání zašle (emailem) autor článku.
Kontakt na autora:
E-mail:
Josef.Tošenovský@vsb.cz
Zveřejněno: Duben 2001